Calculus Problem of the Week July 11 2011

Sometimes easy and sometimes hard, our calculus problem of the week could come from any calculus topic. If you really want to get better at calculus, following these problems is a great way to make yourself practice! Past calculus problems of the week.

This week’s problem:
(click “see the solution” at the bottom of post to, well, see the solution.)
This week we will go with a “routine” limit problem that highlights an aspect of limits people tend to forget!
Without using a graph, find the limit: \lim_{x->-1}\dfrac{x^2+3x+2}{x+1}

See the solution.

The “rule” I have for finding limits is to plug the number in unless something “breaks”. That is, plug the number in and see if I end up with a 0/0. If you try to plug in -1 in this case, you get 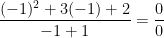\dfrac{(-1)^2+3(-1)+2}{-1+1}=\dfrac{0}{0}. Many people at this stage would assume that the limit doesn’t exist, BUT THAT ISN’T NECESSARILY TRUE! 0/0 is an indeterminate form and getting it is a sign that you need to try another approach.

Luckily, the function we have simplifies nicely: \dfrac{x^2+3x+2}{x+1}=\dfrac{(x+1)(x+2)}{x+1}=x+2. This means that \lim_{x->-1}\dfrac{x^2+3x+2}{x+1}=\lim_{x->-1}(x+2)=-1+2=1.